已知高位攻击

pukr

1. 已知p高位2.2021赣网杯coppersmith
持续更新

pukr

已知P高位：
[对RSA-Factoring with High Bits Known理解](https://www.jianshu.com/p/1a0e876d5929)
这篇文章把原理讲解了，我只会用脚本，格基规约还在学习中.....
以这道CTF题目为例：

1. from Crypto.Util.number import *
   
2. import binascii
   
3. import gmpy2
   
4. flag = '*****************************************'
   
5. hex_flag=int(flag.encode("hex"),16)
   
6. 
   
7. p=getPrime(256)
   
8. q=getPrime(256)
   
9. n=p*q
   
10. 
    
11. e=getPrime(100)
    
12. 
    
13. c=pow(hex_flag,e,n)
    
14. 
    
15. p=((p>>60)<<60)
    
16. 
    
17. print("n=",hex(n))
    
18. print("p=",hex(p))
    
19. print("e=",hex(e))
    
20. print("c=",hex(c))
    
21. '''
    
22. ('n=', '0x558477ce1d081f831cfa159290ee4fd14888422c216a16ad86e2b2d4335e3cb18ed0120a955f970b17b229a8e7d0ae1b6f0c40213ad0e127eba99ae0d8a82397L')
    
23. ('p=', '0x8fbcbb7d1e9f393ee21b537d6e0bd2cf8629e315f4e356c1e000000000000000L')
    
24. ('e=', '0xf7278179324b11fd83d08aa6fL')
    
25. ('c=', '0x36e1c09ccad45cd63a0f07e704d3811c39d70cdfdad999d2df90255a76c58cf6fe99ac1ab1d5d99a4ce1a2ebdbfbc49ce72df2a0b90766ff84ab0ef62068d46bL')
    
26. '''

复制代码

首先通过sage分解n：
[在线运行sage](https://sagecell.sagemath.org/)

1. n = 0x558477ce1d081f831cfa159290ee4fd14888422c216a16ad86e2b2d4335e3cb18ed0120a955f970b17b229a8e7d0ae1b6f0c40213ad0e127eba99ae0d8a82397L
   
2. p_fake = 0x8fbcbb7d1e9f393ee21b537d6e0bd2cf8629e315f4e356c1e000000000000000L
   
3. 
   
4. # pbits = p_fake.nbits()
   
5. pbits = 256
   
6. kbits = 60  #p失去的低位
   
7. pbar = p_fake & (2^pbits-2^kbits)
   
8. print("upper %d bits (of %d bits) is given" % (pbits-kbits, pbits))
   
9. 
   
10. PR.<x> = PolynomialRing(Zmod(n))
    
11. f = x + pbar
    
12. 
    
13. x0 = f.small_roots(X=2^kbits, beta=0.4)[0]  # find root < 2^kbits with factor >= n^0.3
    
14. p= x0 + pbar
    
15. print(p)

复制代码

​​​
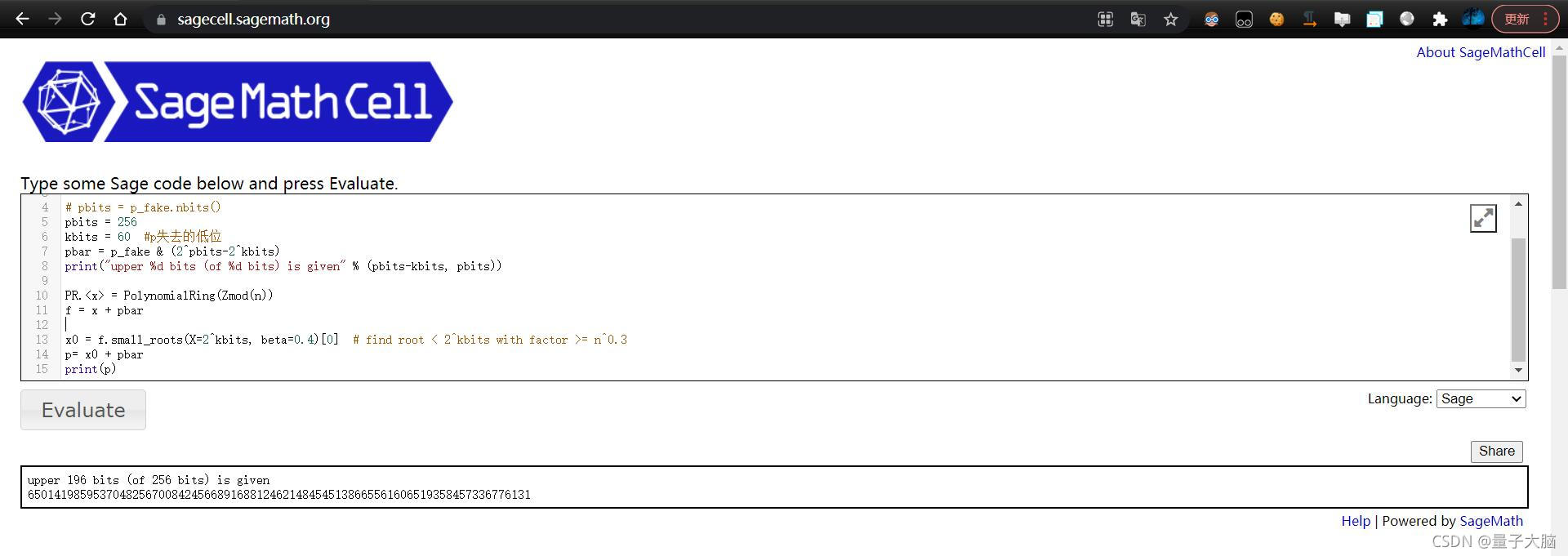
这样就得到了p，接下来就是常规解题了：

1. from Crypto.Util.number import *
   
2. import gmpy2
   
3. import binascii
   
4. # from sage import *
   
5. 
   
6. n = 0x558477ce1d081f831cfa159290ee4fd14888422c216a16ad86e2b2d4335e3cb18ed0120a955f970b17b229a8e7d0ae1b6f0c40213ad0e127eba99ae0d8a82397
   
7. p = 65014198595370482567008424566891688124621484545138665561606519358457336776131
   
8. e = 0xf7278179324b11fd83d08aa6f
   
9. c = 0x36e1c09ccad45cd63a0f07e704d3811c39d70cdfdad999d2df90255a76c58cf6fe99ac1ab1d5d99a4ce1a2ebdbfbc49ce72df2a0b90766ff84ab0ef62068d46b
   
10. pp = binascii.b2a_hex(long_to_bytes(p)).decode()
    
11. print(pp)
    
12. ppp = 0x8fbcbb7d1e9f393ee21b537d6e0bd2cf8629e315f4e356c1e7c5e22d8cff45c3
    
13. q = n // ppp
    
14. phi = (ppp-1)*(q-1)
    
15. d = gmpy2.invert(e, phi)
    
16. m = pow(c, d, n)
    
17. print(long_to_bytes(m))

复制代码