DASCTF八月赛Reverse Writeup

gclome

原文链接：DASCTF八月赛Reverse Writeup

前言
八月赛时候就看了一眼题，没怎么做。这几天复盘总结时候，居然发现没有公开的Writeup，所以有了这篇文章。这次三道题目风格相似，题目之中都有相同的部分，应该是同一个师傅出的。

UR_BAD_BAD
直接拖入IDA，找main函数，F5大法一气呵成。
​
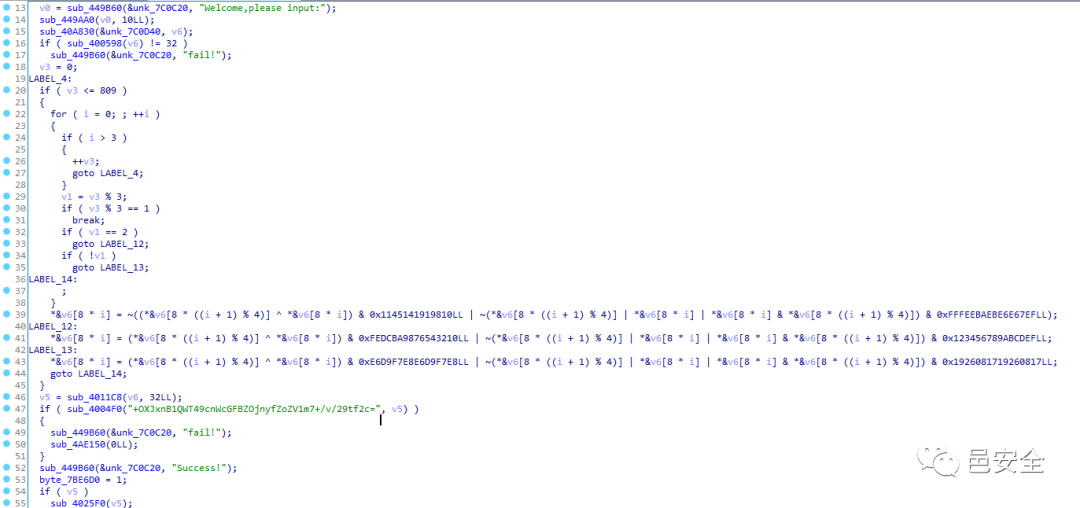
之后就看到这个位运算，看起来还是挺头疼的。但是这里和加密没有半点关系，因为整个main函数流程就是假的。细心观察一下，会发现这里的Welcome的w是大写的。而真正运行起来，w是小写的。
​
这时候说明没有走这个main流程。需要去找到真正的流程，去字符串找一下，看到一些奇怪的字符串。
​
然后通过这个字符串可以找到一段看上去很可疑的代码，但没有被IDA识别为函数。这里被加了花指令，需要我们手动去花。代码太长，写一个idapython的脚本

1. start_addr = 0x4020b3
   
2. end_addr = 0x402DB9
   
3. while(start_addr <= end_addr):
   
4.     if Byte(start_addr) == 0xe8 and Byte(start_addr+1) == 0x3 and Byte(start_addr+2) == 0:
   
5.         for j in range(13):
   
6.             PatchByte(start_addr+j,0x90)
   
7.         start_addr += 13
   
8.         continue
   
9.     start_addr += 1
   
10. 
    
11. print 'success'

复制代码

之后就可以看伪代码了。

​
可以看到第一个调用的函数，就是首先就是在检测是否存在调试器，通过getpid和getppid查找自己的pid和父进程的pid进行比较，来判断是否被调试。（这里可以通过attach绕过）
之后是decode_output，这题为了防止直接查找字符串找到关键信息，将关键信息全部做了编码。输出是需要自行解码。接下来就是输入、求输入的长度、encode、比较。而我们重点分析的地方是encode函数。
​
可以看到这个函数大致看一下其实挺像base64，但table不同，所以猜测可能是base算法，但是是魔改的。静态分析时候可以看到table是01234567!。但如果用这个table，那必不可能过check啊。于是动态调试了一下，发现在一个不起眼的地方，table被改成了0xDktbNB!。这下就好办了。
接下来就是说算法，其实这个算法很简单，和各base算法一样的原理，转ascii，按照二进制截取三位，查表。或许可以叫base8?不知道，2333
算法和table都知道了，写解密算法就很容易了。

1. # -*- coding: utf-8 -*-
   
2. cip = 'Dx0t0bDkD0NbDx0NkNNbktNkkk0txtN0kkDkxbkBxbNNBbkBDx0kDxNkD0NbDx0Nx0DBNt00'
   
3. key = '0xDktbNB'
   
4. index = []
   
5. for i in cip:
   
6.     for j in range(len(key)):
   
7.         if i == key[j]:
   
8.             index.append(j)
   
9. text = []
   
10. for i in index:
    
11.     text.append((bin(i)[2:]).zfill(3))
    
12. f = []
    
13. for i in range(0,len(text),8):
    
14.     j = 0
    
15.     tmp = ''
    
16.     while j <= 7:
    
17.         tmp += text[i+j]
    
18.         j += 1
    
19.     f.append(tmp)
    
20. flag = ''
    
21. for i in range(len(f)):
    
22.     flag += hex(int(f[i],2))[2:].decode('hex')
    
23. print flag

复制代码

hide_and_seek
这次是Windows下的。可以在export这里看到TLS，而TLS是在main函数之前执行的。可能会存在一些反调试之类的东西。
​
如果有反调试的话，可以从导入表中找是否有IsDebuggerPresent这个函数，这次还真有。查看调用的地方。
​
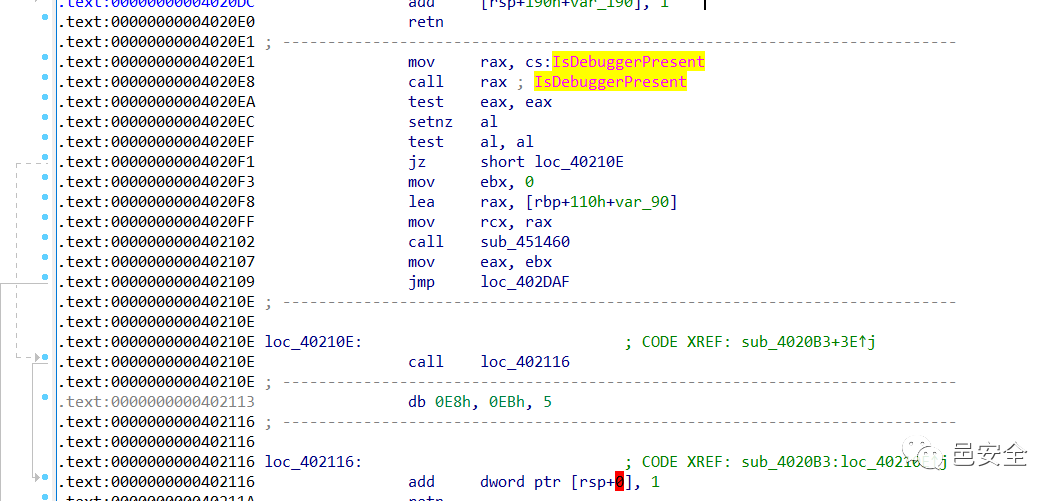
也是加了花指令，和上个题目的一样，用脚本去掉。然后看下伪代码。（可能分析伪代码时候会出现call analysis all的问题，只需要进对应的地址进子函数中把子函数中的代码转换成伪代码，再出来就不会报错了）
​
前边的逻辑大致好看一些，就是解密输出字符串，输入，判断flag格式和长度。但后边这段就不大好分析，中间也不难分析就是取前八位进行了一个运算，然后做比较。
​
而在sub_474370函数里边，感觉就有些混乱，而且这里貌似还有一个处理异常的反调试（我tcl没弄明白Orz）不过问题不大，可以跳过，但是跳过的同时也跳过了加密的具体过程，好在发现sub_474370之后的sub_471ab0是check函数，两个参数分别位自己输入后的加密和密文。
​
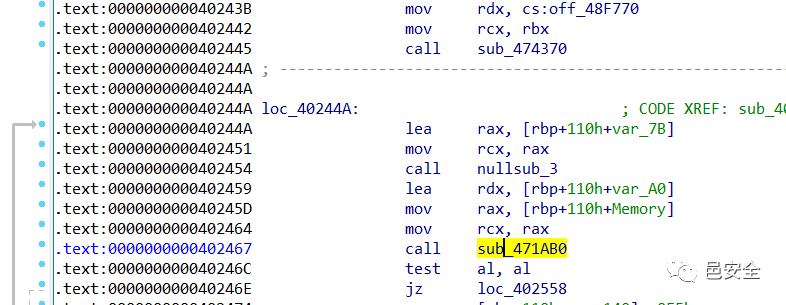
那么这时候就只能猜算法了，多次测试发现，每一位不会影响下一位，且小幅度变化输入对密文的影响也不大，也没发现很长的代码。就猜测是+-^等运算，经测试发现为xor运算，可以通过输入把xor的key套出来，之后xor密文得到flag。

1. # -*- coding: utf-8 -*-
   
2. cip1 = [0x12,0xFE,0xCB,0x94,0x61,0x3D,0x06,0xE3,0xBF,0x88,0x55,0x31,0x01,0xD7,0xA0,0x7C,0x49,0x30,0xFE,0xAD,0x58,0x07,0xC2,0x71,0x2F,0xEA,0x99,0x44,0x01,0xC1,0x6C,0x1B,0xD6,0x85,0x12,0xFE]
   
3. key1 = [1]*36
   
4. cipher = [0x75,0x93,0xAB,0xF2,0x1B,0x54,0x36,0x86,0x8D,0xD6,0x35,0x5E,0x64,0x89,0xD2,0x4E,0x7B,0x5A,0xA0,0xEB,0x0A,0x59,0xA5,0x41,0x40,0x8F,0xC7,0x31,0x68,0xF3,0x32,0x77,0xB6,0xB5,0x7D,0x82]
   
5. flag = ''
   
6. for i in range(len(cipher)):
   
7.     flag += chr(cip1[i]^key1[i]^cipher[i])
   
8. print flag

复制代码

STABLE_TRICK
这题也发现了TLS，但是找了半天没发现有什么奇怪的地方。main函数逻辑也很简单。

​
那就先逆逆main函数再说吧。需要关注的函数就是图中注释的三个，先看一下第一个xor的函数。
​
基本是异或生成的，所以基本可以认定flag的长度为20位。
第二个函数
​
后四位给出像是一种提示。
第三个函数
​
又是这个表达式。但其实在这里没什么用，真正的加密是在sub_401850中，其他都是用来迷惑的。
​
而在sub_401850中，经历了一系列的加和xor，还有矩阵行列变换进行了加密，感觉不像是一种现有的加密算法，由之前的16位数据、4位已知key和刚才没有注意的0xFFBEADDE生成了十六位数据并进行base64。于是我大致了解了逻辑之后，开始还原加密算法并写出解密算法。这里就可以直接看代码了，不用多说。

1. # -*- coding: utf-8 -*-
   
2. input_num = [0x9A,0xCE,0xFD,0x07, \
   
3.         0x01,0x0E,0x0C,0x02, \
   
4.         0x0C,0x0D,0x24,0x2A, \
   
5.         0x24,0x26,0x24,0x22 \
   
6.         ]
   
7. def encrypt(input_num):
   
8.     sum = []
   
9.     for i in range(0,len(input_num),4):
   
10.         sum.append((input_num[i+3]<<24)+(input_num[i+2]<<16)+(input_num[i+1]<<8)+input_num[i])
    
11. 
    
12.     for k in range(1):
    
13.         tmp = k%3
    
14.         if tmp == 0:
    
15.             sum[0] = sum[0]^0x6560773b
    
16.             sum[1] = sum[1]^0xffbeadde
    
17. 
    
18.             sum[0],sum[2] = sum[2],sum[0]
    
19.             sum[1],sum[3] = sum[3],sum[1]
    
20. 
    
21.         if tmp<=1:
    
22.             sum[0] = sum[0]^0x6560773b
    
23.             sum[1] = sum[1]^0xffbeadde
    
24. 
    
25.             tmp_num = []
    
26.             for i in range(len(sum)):
    
27.                 tmp_num.append(sum[i]&0xff)
    
28.                 tmp_num.append((sum[i]>>8)&0xff)
    
29.                 tmp_num.append((sum[i]>>16)&0xff)
    
30.                 tmp_num.append((sum[i]>>24)&0xff)
    
31. 
    
32.             input_num = []
    
33.             for i in range(0,4):
    
34.                 for j in range(0,4):
    
35.                     input_num.append(tmp_num[i+4*j])
    
36.             flag = 0
    
37.             flag = (sum[0]+0x6560773b)/0x100000000
    
38.             sum[0] = (sum[0]+0x6560773b)&0xffffffff
    
39.             sum[1] = (sum[1]+0xffbeadde+flag)&0xffffffff
    
40. 
    
41.             sum[0],sum[2] = sum[2],sum[0]
    
42.             sum[1],sum[3] = sum[3],sum[1]
    
43. 
    
44.         if tmp <= 2:
    
45.             flag = 0
    
46.             flag = (sum[0]+0x6560773b)/0x100000000
    
47.             sum[0] = (sum[0]+0x6560773b)&0xffffffff
    
48.             sum[1] = (sum[1]+0xffbeadde+flag)&0xffffffff
    
49. 
    
50.             sum[0],sum[2] = sum[2],sum[0]
    
51.             sum[1],sum[3] = sum[3],sum[1]
    
52. 
    
53.     for i in range(len(input_num)):
    
54.         print hex(input_num[i])
    
55. def decrypt(cip_num):
    
56.     #cip_num = [0xd8,0x78,0x7c,0xfa,0xb2,0x2c,0xe8,0xf4,0x41,0xee,0x12,0x93,0x6,0xe2,0xa2,0x2]
    
57.     tmp_num = []
    
58. 
    
59.     sum = []
    
60.     # 63
    
61.     for i in range(0,4):
    
62.         for j in range(0,4):
    
63.             tmp_num.append(cip_num[i+4*j])
    
64.     for i in range(0,len(tmp_num),4):
    
65.         sum.append((tmp_num[i+3]<<24)+(tmp_num[i+2]<<16)+(tmp_num[i+1]<<8)+tmp_num[i])
    
66. 
    
67.     sum[0] = sum[0]^0x6560773b
    
68.     sum[1] = sum[1]^0xffbeadde
    
69.     sum[0],sum[2] = sum[2],sum[0]
    
70.     sum[1],sum[3] = sum[3],sum[1]
    
71.     sum[0] = sum[0]^0x6560773b
    
72.     sum[1] = sum[1]^0xffbeadde
    
73.     # 62
    
74.     for k in range(62,-1,-1):
    
75.         tmp = k%3
    
76.         if tmp <= 2:
    
77.             sum[0],sum[2] = sum[2],sum[0]
    
78.             sum[1],sum[3] = sum[3],sum[1]
    
79. 
    
80.             flag = 0
    
81.             sum[0] = (sum[0]-0x6560773b)&0xffffffff
    
82.             flag = (sum[0]+0x6560773b)/0x100000000
    
83.             sum[1] = (sum[1]-flag-0xffbeadde)&0xffffffff
    
84. 
    
85.         if tmp <= 1:
    
86.             sum[0],sum[2] = sum[2],sum[0]
    
87.             sum[1],sum[3] = sum[3],sum[1]
    
88. 
    
89.             flag = 0
    
90.             sum[0] = (sum[0]-0x6560773b)&0xffffffff
    
91.             flag = (sum[0]+0x6560773b)/0x100000000
    
92.             sum[1] = (sum[1]-flag-0xffbeadde)&0xffffffff
    
93. 
    
94.             tmp_num = []
    
95.             for i in range(len(sum)):
    
96.                 tmp_num.append(sum[i]&0xff)
    
97.                 tmp_num.append((sum[i]>>8)&0xff)
    
98.                 tmp_num.append((sum[i]>>16)&0xff)
    
99.                 tmp_num.append((sum[i]>>24)&0xff)
    
100. 
     
101.             cip_num = []
     
102.             for i in range(0,4):
     
103.                 for j in range(0,4):
     
104.                     cip_num.append(tmp_num[i+4*j])
     
105. 
     
106.             sum[0] = sum[0]^0x6560773b
     
107.             sum[1] = sum[1]^0xffbeadde
     
108. 
     
109.         if tmp == 0:
     
110.             sum[0],sum[2] = sum[2],sum[0]
     
111.             sum[1],sum[3] = sum[3],sum[1]
     
112. 
     
113.             sum[0] = sum[0]^0x6560773b
     
114.             sum[1] = sum[1]^0xffbeadde
     
115. 
     
116.     data = []
     
117.     for i in range(len(sum)):
     
118.         data.append(sum[i]&0xff)
     
119.         data.append((sum[i]>>8)&0xff)
     
120.         data.append((sum[i]>>16)&0xff)
     
121.         data.append((sum[i]>>24)&0xff)
     
122.     data += [0x65,0x60,0x77,0x3b]
     
123.     xor_decry(data)
     
124. def xor_decry(data):
     
125.     flag = ''
     
126.     flag += chr(data[0]^0xab)
     
127.     flag += chr(data[0]^data[1]^0x66)
     
128.     tmp = data[1]
     
129.     for i in range(2,5):
     
130.         t = data[i]
     
131.         data[i] ^= tmp
     
132.         flag += chr(data[i])
     
133.         tmp ^= t
     
134.     for i in range(5,10):
     
135.         t = data[i]
     
136.         data[i] ^= tmp^0xd
     
137.         flag += chr(data[i])
     
138.         tmp ^= t ^ 0xd
     
139.     for i in range(10,20):
     
140.         t = data[i]
     
141.         data[i] ^= tmp ^ 0x25
     
142.         flag += chr(data[i])
     
143.         tmp ^= t^0x25
     
144.     print flag
     
145. if __name__ == '__main__':
     
146.     #encrypt(input_num)
     
147.     cip_num = [0xae,0xd9,0xa1,0x50,0x7a,0xe1,0xf8,0xe3,0x43,0x83,0xb0,0xb0,0x17,0x9f,0xcd,0x30]
     
148.     decrypt(cip_num)

复制代码